Mechanics Graphing calculator on Parallelogram law of forces

In Mathematics, The parallelogram law of forces : If two forces are acting at a point that are represented in magnitude and direction by the two sides of a parallelogram drawn from one of its angular point, then their resultant force is represented both in magnitude and direction by the diagonal of the parallelogram passing through that angular point. For drawing graph resultant force by the law of law of parallelogram of forces with the free graph drawing website www.graph2d.com, type 20 in the input box of force1 with coresponing angle in degree 15 and again type 12 in the input box of force2 with coresponing angle in degree 60, then the graph will drawn automatically of parallelogram with resultant force and direction. The graph is given belows.

---

For learn about Piecewise function of Mathematics and graphing, visit: Graphing Piecewise function of Math.

1. Newton's First law of motion : An object at rest remains at rest or an object in motion remains in motion at constant speed in a straight line unless acted on by an unbalanced force. As for example, A ball rolling down a hill will continue to roll unless friction or another force stops it.
2. Newton's second law of motion : The acceleration of an object depends on the mass of the object and the amount of force applied. When a body is acted upon by a net force, the body's acceleration multiplied by its mass is equal to the net force i.e F=ma. As for example, suppose you are riding a bycycle. The total weight of you and your bycycle is the mass. Your leg muscles pushing on the pedals of your bicycle is the force. When you push on the pedals, your bicycle accelerates. when you are increasing the speed of the bicycle by applying force to the pedals, then the acceleration is also increase.
3. Newton's third law of motion : When an object exerts a force on another object, the second object exerts an equal and opposite force on the first object. As for example, when a ball fall down the ground, the ball applies an action force on the ground. The ground applies a reaction same force with opposite direction and hence the ball bounces back.

Statement of Triangle law of forces : If two forces acting at a point are represented in magnitude and direction by the two adjacent sides of a triangle taken in order, then the third side or closing side of the triangle taken in the reversed order represents the resultant of the forces in magnitude and direction.

Here △ABC is a triangle and two forces P and Q acting at a point B are represented in magnitude and direction by the two adjacent sides sides AB and BC of the triangle △ABC taken in order, then the third side or closing side AC of the triangle △ABC taken in the reversed order represents the resultant of the forces R in magnitude and direction.

Statement of Lami’s theorem of forces : If three forces acting at a point are in equilibrium, then each force will be proportional to the sine of the angle between the other two forces. From the bellows figure, there are three forces P, Q and R acting to the point O with the direction OA, OB and OC respectively. So by the Lami’s theorem , we can write P/sin∠BOC=Q/sin∠AOC=R/sin∠AOB. The three forces must be coplanar and the three forces must be concurrent.

Statement of Varignon's Theorem : This theorem is also koown as the principle of moments of forces which is very useful tool in scalar moments calculations.If a number of coplanar forces are acting on a body, then the algebraic sum of their moments about a point in their plane is equal to the moment of their resultant about the same point. From the bellows figure, the forces P and Q are acting on a point A and O is another point. So The Moment Of R About O = (The Moment Of P About O + The Moment OF Q About O).

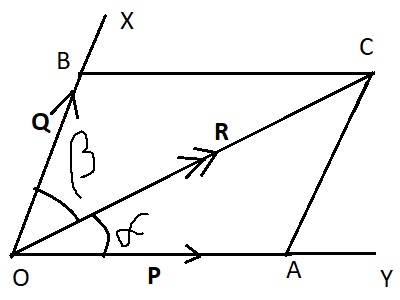
Any force can be broken down into components along a specific direction or axis, the broken component is called projection of the force along that specific direction or axis. The projection can help us to analyze how much of the force is influencing motion or stress in a particular direction. Let us consider two force P, Q and α is an angle between them. Then the projection of P on Q = (P.Q)/Q=PQcosα /Q=Pcosα and the projection of Q on P = (P.Q)/P=PQcosα /P=Qcosα where P and Q are magnitude of the force P and Q respectively.

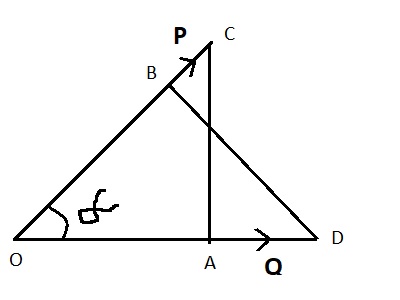
From △OAC, cosα=OA/OC ⇒OA = OC cosα ⇒projection of P on Q = Pcosα
and from △OBD, cosα=OB/OD ⇒OB = OD cosα ⇒projection of Q on P = Qcosα
In a physical context, the projection is useful in determining how much of the force contributes to deformation or movement along a certain line or plane. For instance, in resolving forces along inclined planes, the projections help us separate the force into parallel and perpendicular components.

Uses of projection of a force:

The projection of a force is essential in many areas of engineering, mathematics, physics and mechanics because it help us to simplify the complex force systems into manageable components. Some uses of the projection of a force are Analyzing Motion on Inclined Planes,Calculating Work Done by a Force, Structural Analysis and Load Distribution, Torque and Rotational Motion,Electrical and Magnetic Force Analysis, Resolving Forces in Multi-Directional Systems, Determining Normal and Tangential Forces, Fluid Dynamics and Aerodynamics

Statement of Polygon law of Forces of Composition : If n-1 forces acting at a point are represented in magnitude and order by the (n-1) sides of an n-sides polygon taken in the same direction, their resultant force is represented in magnitude and direction by the n-th side of the polygon taken in the opposite order.

Here OA+AB+BC+CD=OD

Let us consider a force R and its resolved parts are P and Q along OX and OY respectively. The angle between P and R is α and The angle between Q and R is Β

Then by determination of components of a force in a fixed direction or sine law of forces are P=RsinΒ/sin(α+Β) and P=Rsinα/sin(α+Β) along OX and OY respectively.
The vertical resolved part = Rsnθ and the horizontal resolved part = Rcosθ

Statement of the Theorem on Resolved Parts of forces: The algebraic sum of the resolved parts of two forces acting at a point in a given direction is equal to the resolved part of their resultant in the same direction.
Let us consider two forces are P and Q along OX and the resultant force is F along OX , then by the Theorem on Resolved Parts of forces is P+Q=R.

Statement of (m, n) theorem of mechanics or m-n theorem of mechanics or m:n theorem of mechanics :

If two forces m.OA and n.OB (m>0,n>0) acts at the point O in the direction of OA and OB respectively, then their resultant force is (m+n).OC where C is a point on the line AB and m.AC=n.BC.

Like Parallel Forces :

If twoor more parallel forces acts in the same direction, then the forces are called the like parallel forces. In the Figure, P and Q are like parallel forces.

Ulike Parallel Forces :

If twoor more parallel forces acts in the opposite direction, then the forces are called the unlike parallel forces. In the Figure, R and S are unlike parallel forces.

Resultant of Like Parallel Forces :

The resultant force of like parallel forces is their algebraic sum. The direction of the resultant force of like parallel forces is same as the both of parallel forces. The point of action of the resultant parallel forces is find out by the product of magnitude of a force and distance from the point of action to the same force along joining the action of points of two forces is equal to the product of magnitude of another force and another distance from the point of action to the this force along joining the action of points of two forces. In the Figure, P and Q are two forces acting at A and B. Their resultant force acting at C inside AB and beside the big force. We can find the position of C from P.AC=Q.BC.

Resultant of Unike Parallel Forces :

The resultant force of unlike parallel forces is their algebraic subtraction from big force to small force. The direction of the resultant force of unlike parallel forces is same as the big of parallel forces. The point of action of the resultant unlike parallel forces is find out by the product of magnitude of a force and distance from the point of action to the same force along joining the action of points of two forces is equal to the product of magnitude of another force and another distance from the point of action to the this force along joining the action of points of two forces. In the Figure, P and Q are two forces acting at A and B. Their resultant force acting at C which is outside of AB and beside the big force. We can find the position of C from P.AC=Q.BC.

All Formula of a particle moving along a straight line with constant acceleration are given below-

1. v=u+ft where u is initial velocity, v is ending velocity and f is uniform acceleration.
2. s=ut+(1/2)ft² where u is initial velocity, s is distance at time t and f is uniform acceleration .
3. v²=u²+2fs where u is initial velocity, v is ending velocity, s is distance at time t and f is uniform acceleration .
4. s_th=u+(1/2)f.(2t-1) where u is initial velocity, s is distance at t-th second and f is uniform acceleration .

All Formula of a particle moving along a straight line with constant retardation are given below-

1. v=u-ft where u is initial velocity, v is ending velocity and f is uniform retardation.
2. s=ut-(1/2)ft² where u is initial velocity, s is distance at time t and f is uniform retardation.
3. v²=u²-2fs where u is initial velocity, v is ending velocity, s is distance at time t and f is uniform retardation.
4. s_th=u-(1/2)f.(2t-1) where u is initial velocity, s is distance at t-th second and f is uniform retardation.

All Formulae of a particle moving along a straight line with gravitational acceleration and falling particle freely from the upper position are given below-

1. v=gt where u=0 is initial velocity, v is ending velocity and g is gravitational acceleration.
2. h=(1/2)gt² where u is initial velocity, h vertical is distance at time t and g is gravitational acceleration .
3. v²=2gh where u is initial velocity, v is ending velocity, h is vertical distance at time t and g is gravitational acceleration .
4. h_th=(1/2)g.(2t-1) where u is initial velocity, h_th is distance at t-th second and g is gravitational acceleration .

All Formula of a particle moving along a straight line with against gravitational acceleration upward from the earth are given below-

1. v=u-gt where u is initial velocity, v is ending velocity, t is time and g is gravitational acceleration.
2. h=ut-(1/2)gt² where u is initial velocity, h is vertical distance or hight at time t and g is gravitational acceleration .
3. v²=u²-2gh where u is initial velocity, v is ending velocity, h is vertical distance or hight at time t and g is gravitational acceleration .
4. h_th=u-(1/2)g.(2t-1) where u is initial velocity, h_th is distance or hight at t-th second and g is gravitational acceleration .

All Formula of a particle moving along a straight line with gravitational acceleration are given below-

1. v=u+gt where u is initial velocity, v is ending velocity, t is time and g is gravitational acceleration.
2. h=ut+(1/2)gt² where u is initial velocity, h is vertical distance or hight at time t and g is gravitational acceleration .
3. v²=u²+2gh where u is initial velocity, v is ending velocity, h is vertical distance or hight at time t and g is gravitational acceleration .
4. h_th=u+(1/2)g.(2t-1) where u is initial velocity, h_th is verticle distance or hight at t-th second and g is gravitational acceleration .

All Formula of a particle moving along a straight line with against gravitational acceleration from constant hight and upward from the earth are given below-

1. v=-u+gt where u is initial velocity, v is ending velocity, t is time and g is gravitational acceleration.
2. h=-ut+(1/2)gt² where u is initial velocity, h is vertical distance or hight at time t and g is gravitational acceleration .
3. v²=u²+2gh where u is initial velocity, v is ending velocity, h is vertical distance or hight at time t and g is gravitational acceleration .
4. h_th=-u+(1/2)g.(2t-1) where u is initial velocity, h_th is verticle distance or hight at t-th second and g is gravitational acceleration .

Maximum Height or Greatest Height and Total time of flight by a Particle Projected Upward against gravitational acceleration:

1. Maximum Height=u²/(2g) where u is initial velocity and g is gravitational acceleration.

2. Total time of fligt=2u/g where u is initial velocity and g is gravitational acceleration.

3. Rising time= Falling time=u/g where u is initial velocity and g is gravitational acceleration.

1. Maximum Height=u²sin²α/(2g) where u is initial velocity, α is an angle with the horizon and g is the gravitational acceleration.

2. Total time of fligt=2usinα/g where u is initial velocity, α is an angle with the horizon and g is the gravitational acceleration.

3. Horizontal Range=u²sin²α/g where u is initial velocity, α is an angle with the horizon and g is the gravitational acceleration.

4. Rising time= Falling time=usinα/g where u is initial velocity, α is an angle with the horizon and g is the gravitational acceleration.

5. Maximum Range R_max=u²/g where u is initial velocity and g is the gravitational acceleration.