This is an online educational tools of Complex Graphing calculator to create graph of mathematical complex numbers or functions of 2D in this section.There are three portions in this section. For First portion, you can select any of RealNum, Mod,Arg,Re, Im which are real number, modulus, argument, real part, imaginary part of complex number of 1st input box. then select any one of +, -, < and then you can done similarly for Second and Third portions. Then press the drawing button. It takes sometimes to draw graph of this function and be patience to calculate huge points to draw the graph. For zoom this graph, you can change the x-scale and y-scale. It can draw any complex number or function of equation or inequality.It has some limitations such as you can type with z, z^2, z^3, 1/z, conjz and any complex number e.g. 5+3i.Here conjz means conjugate number of z.Thank you for viewing this article.
To get update website, you can clear your browser chache data (if you browse this website before many days) or browse this website with another website browser. Steps for clear chache: 1. on your computer, open browser. 2. At the top right, click More. 3. Click More tools. Clear browsing data. 4. choose a time range. 4. "Cached images and files," check the boxe. 5. Click Clear data. Different browser may have different ways.
Imaginary Number : The square root of a negative real number is called Imaginary Number. The Unit of imaginary number is denoted by i=√(-1). As for example, √(-9)=3i.
Complex Number : The Complex Number is defined by a+ib where a and b are real numbers and i=√(-1). As for example, 3+5i is a Complex Number.
Conjugate Complex Number : If z=x+iy be a Complex Number, then z=x-iy is called the Conjugate Complex Number of complex number z. It is denoted by z=x-iy. As for example, If z=5+4i, then z=5-4i and If z=-3-6i, then z=-3+6i.
Modulas : If z=x+iy be a Complex Number and x=rcosθ, y=rsinθ, then r=|z|=√(x2+y2) is called the modulas of z. As for example, If z=3+4i, then Modulas |z|=√(32+42)=5.
Argument : If z=x+iy be a Complex Number and x=rcosθ, y=rsinθ, then θ=tan-1(y/x) is called the Argument of z. As for example, If z=1+i, then Argument θ=tan-1(1/1)=450.
Real part : If z=x+iy be a Complex Number, then x is called the Real part of complex number z. It is denoted by Re(z)=x. As for example, If z=7+4i, then Re(z)=7.
Imaginary part : If z=x+iy be a Complex Number, then x is called the Imaginary part of complex number z. It is denoted by Im(z)=y. As for example, If z=7+4i, then Im(z)=4.
Argand plane : The set C of complex numbers is naturally identified with the plane R2. This plane is called the Argand plane. A complex number z = x+i y, its real and imaginary parts x and y define an element (x, y) of R2.
Reciprocal of a Complex Number : The reciprocal of a complex number is a complex number which is calculating 1 divided by that complex number. For example, the reciprocal of a complex number 1+i is 1/(1+i)=(1-i)/{(1+i)(1-i)}=(1-i)/(1-i2)=(1-i)/{(1-(-1)}=(1-i)/2=1/2-i/2
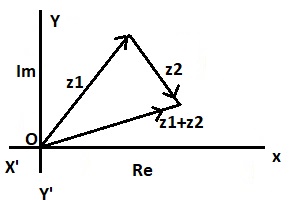
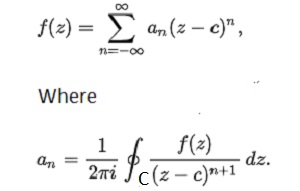The equation of ellipse of complex number system is |z-z1|+|z-z2|=constant. As for example, |z+3+8i|+|z-3-8i|=18 is an equation of ellipse of complex number. For learn about simple function of Mathematics and graphing, visit: Graphing simple function of Mathematics
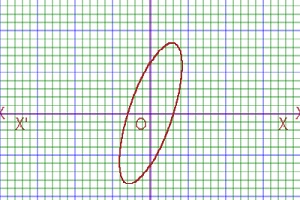
The equation of Hyperbola of complex number system is |z-z1|-|z-z2|=constant. As for example, |z+5i|-|z-5i|=12 is an equation of hyperbola of complex number. For learn about piecewise function and graphing, visit: Graphing piecewise function of Mathematics
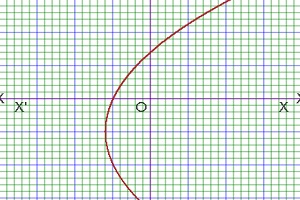
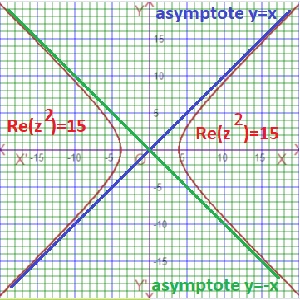
Another equation of Hyperbola of complex number system are Re(z2)=constant and Im(z2)=constant . As for example, Im(z2)=15 is an equation of hyperbola of complex number. For learn about implicit function and graphing, visit: Graphing Implicit function of Mathematics
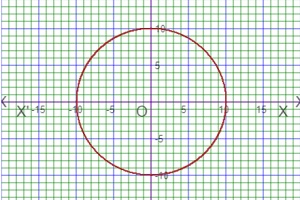
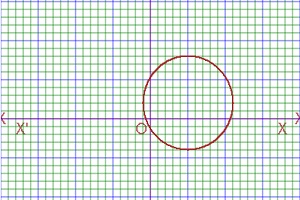
The equation of Circle of complex number system is |z-z1|=constant. As for example, |z-5-2i|=6 is an equation of circle of complex number. For learn about linear programmming of Mathematics and graphing, visit: Graphing linear programmming of Mathematics
The inequality of ring shape region of complex variable 3<=|z+3i|<=5 is given bellow and.
Youtube vedio tutorial for complex analysis.
For learn about inequality of Mathematics and graphing, visit: Graphing Inequality of Mathematics
The inequality of outer region of hyperbola of complex variable Re(z2)>2 is given bellow-
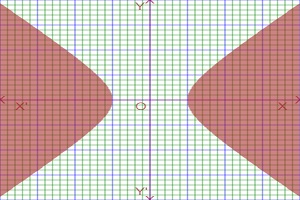
For learn about polar function of Mathematics and graphing, visit: Graphing Polar function of Mathematics
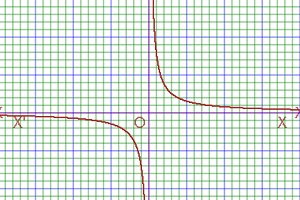
The inequality of outer region of hyperbola of complex variable Im(z2)>2 is given bellow-
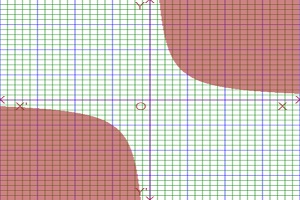
For learn about parametric function of Mathematics and graphing, visit: Graphing Parametric function of Mathematics
Definition of Comlex analysis
The Complex analysis is the study of analysis of Complex Numbers together with their graphs, derivatives,integrations, manipulation and other mathematical properties. Complex analysis is also known as one of the classical branch of mathematics and analysis. The Complex Numbers with their functions and their graphs, limits, derivatives, integrations, manipulation and other mathematical properties. The
The Complex analysis is a mathematical topic of practical applications to solve physical problems. The real life applications of complex analysis are Signal processing, AC circuit analysis,
The Quantum mechanics,
The Electronics,
The Electromagnetism,used in
The computer science engineering,used in mechanical and
The civil engineering, used in
The control systems, etc.
Euler's formula or Euler's theorem of Complex analysis:
If i is the unit of imaginary number and where e is the base of the natural logarithm, Then the Euler's formula or Euler's theorem of Complex analysis is defined by eiθ=cosθ+isinθ where θ is a angle. The Euler's formula or Euler's theorem , named from Swiss Mathematician Leonhard Euler. The Euler's formula or Euler's theorem of Complex analysis establishes the fundamental relationship between the complex exponential function and the trigonometric functions i.e. eix;=cosx+isinx where e is the base of the natural logarithm and i is the unit of imaginary number.
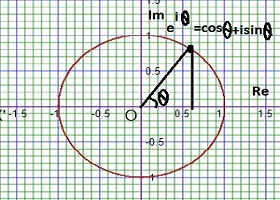
De Moiver’s Theorem of Complex analysis:
If i is the unit of imaginary number, Then the De Moiver’s Theorem of Comlex analysis is defined by (cosx+isinx)n=cosnx+isinnx where x is a angle and n is any integer. The theorem , named from The Mathematician Abraham de Moivre.
The relation between Euler's formula and De Moiver’s Theorem of Complex analysis is De Moivre's formula is a precursor to Euler's formula. Anyone can derive de Moivre's formula by applying the Euler's formula and the exponential law of integer i.e. (eix)n=einx=cosnx+isinnx .
:If z1 and z2 are two complex numbers and |z1|,|z2| and |z1 + z2| are modulus of z1, z2 and z1+z2 respectively, then the Triangle Inequality of complex numbers is |z1 + z2|≤|z1| + |z2|. This theorem is generalized by |z1 + z2 + z3+....+zn|≤|z1| + |z2|+|z3|+.....+|zn|.
Parametric equation of a circle of complex number on complex plane is z(t)=rcost+irsint=reit where 0≤t≤2π and r is the radius of the circle. As for example,z(t)=10cost+10isint=10eit where 0≤t≤2π is a circle of radius 10 units and the center is origin. The general equation of a circle is x2+y2+2gx+2fy+c=0 where the center is (-g, -f), so the parametric general equation of the circle on complex plane will be z(t)=(-g+rcost)+i(-f+rsint).
The general equation of an ellipse is x2/a2+y2/b2=1 where the center is (0, 0), so the parametric equation of the ellipse on complex plane will be z(t)=(acost)+i(bsint) where 0≤t≤2π.
The general equation of a hyperbola is x2/a2-y2/b2=1 where the center is (0, 0), so the parametric equation of the hyperbola on complex plane will be z(t)=(asect)+i(btant) where 0≤t≤2π.
The general equation of a parabola is y2=4ax, so the parametric equation of the parabola on complex plane will be z(t)=(at2)+i(2at) where 0≤t≤2π.
N.B: If you want to drawing graph of parametric equation on complex plane, you will use graphing parametric calculator on complex plane.