Free Graphing piecewise function calculator of math

The piecewise function is defined by multiple sub-functions, where the sub-function are in defined as the different interval in the Domain. As for example,

For sketching the graph of modulus or absolute value function with piecewise function calculator, the graph of the right side of y axis (x>=0) is a straight line y=x and the graph of the left side of y axis(x < 0 ) is a straight line y=-x. Both part of the graph is situated on the upper side of x-axis. For sketching this graph with online free website www.graph2d.com, type x in the first row first input box and the condition x>=0 in 2nd input box. Again type -x in the second row first input box and the condition x< 0 in 2nd input box, then the graph will drawn automatically of the modulus function

For more learn, visit: Practice for graphing piecewise functions of math. Graphing absolute value function calculator can run any device and any website browser.

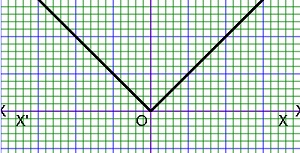
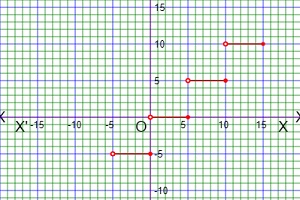
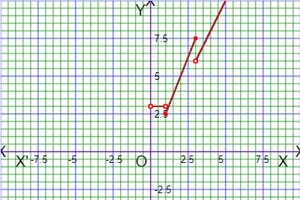
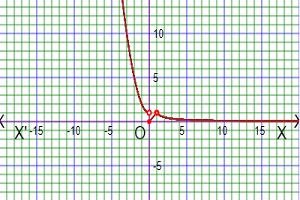
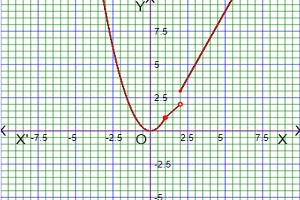
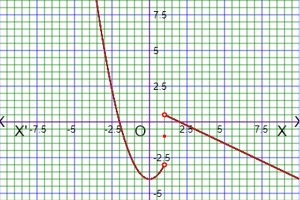
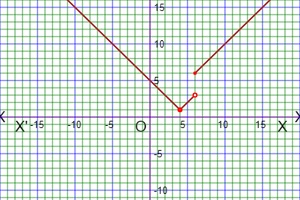
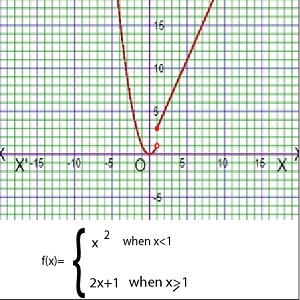
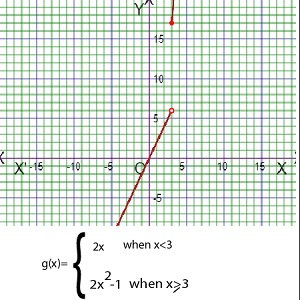
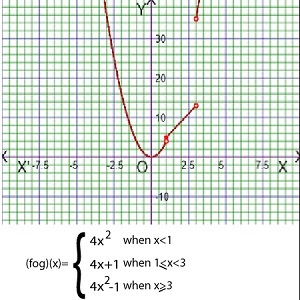
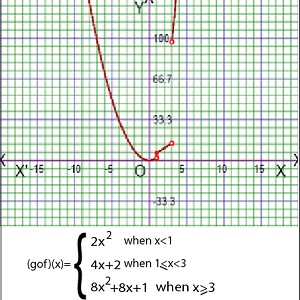
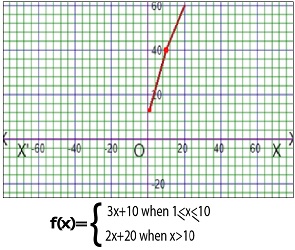
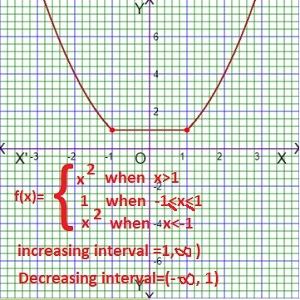
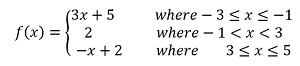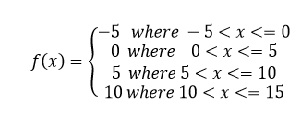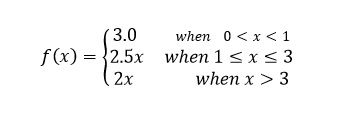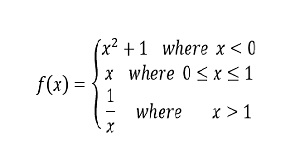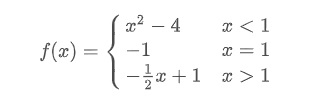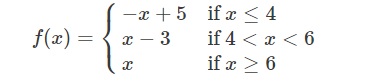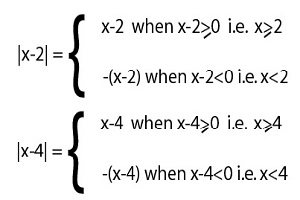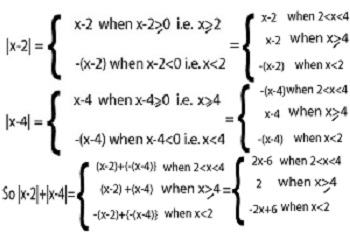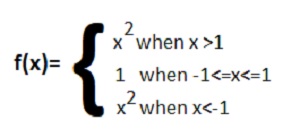As for example, a piecewise function is given bellows-

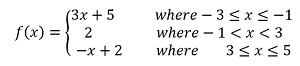
For sketching with 3 piecewise function calculator, type in 1st row left side 3x+5 and right side -3<=x<=-1, type in 2nd row left side 2 and right side -1<x<3 and type in 3rd row left side -x+2 and right side 3<=x<=5, then you can get the 3 piecewise function graph.

For finding the value of f(-2), f(-1), f(0) and f(4), we will check the values of x is situated in which intervals . If x=-2,then it is situated in the 1st interval and this interval corresponding to the function 3x+5, so f(-2)=3(-2)+5=-6+5=-1. If x=-1,then it is situated in the 1st interval and this interval corresponding to the function 3x+5, so f(-1)=3(-1)+5=-3+5=2. If x=0,then it is situated in the 2nd interval and this interval corresponding to the constant function 2, so f(0)=2. If x=4,then it is situated in the 3rd interval and this interval corresponding to the function -x+2, so f(4)=-4+2=-2. The graph of the given function is given belows.

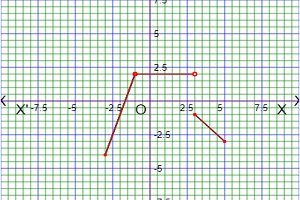
We can find out the Domain and Range of the function from the graph. At first we check the graph is situated what interval along x-axis for Domain. We can see the graph is situated in the interval [-3, 5], so Domf=[-3, 5]. Again we check graph is situated what interval along y-axis for Range. We can see the graph is situated in the interval [-4, 2], so Domf=[-4, 2].

For more learn, visit: Practice for graphing piecewise functions of math. Graphing piecewise functions calculator can run any device and any website browser.

The piecewise function another example,

For sketching the graph of Piecewise function with piecewise function calculator , there are four input boxes for four sub-functions in left side and another four input boxes for corresponding conditions in right side. For sketching this graph with online free graph drawing website www.graph2d.com, type 2x+15 in the first row first input box and the condition x< -5 in 1st row 2nd input box. Again type abs(x) in the second row first input box and the condition -5<=x<=5 in 2nd row 2nd input box.Again type -2x+15 in the 3rd row first input box and the condition x>=5 in 3rd row 2nd input box. Then the graph will drawn automatically of that piecewise function

Step function or Staircase function f : R->R is a types of piecewise constant function which has finite number of pieces. As for example, consider a step function or a staircase function.

This Step function or Staircase function's Domain =(-5,0]U(0,5]U(5,10]U(10,15]=(-5,15] , Range ={-5,0,5,10} and the graph of this step function or staircase function is given belows.

Step function graphing calculator can run any device and any website browser.

For uses or application or real life example on piecewise function , we can consider taxicab fare. let initial fare of a taxicab is 3.0 $ for less than 1 km, Short trip fare is 2.5 $ per km for 1km to 3 km and long trip fare is 2.0 $ per km for grater than 3 km. For this situation, we can make a 3 piecewise function is given belows.

Here x is denoted as total km and f(x) is toal taxicab fares. Now a passenger is going to a short trip for 2 km, then the total taxcab fare will be f(2)=2X2.5=5 $ and another passenger is going to long trip for 12 km, then total fare will be f(12)=2X12=24 $

Graph of this piecewise function (Drawing with piecewise function calculator ) is given bellows which is Uses or Application or Real life example on piecewise function

As for example, consider a piecewise function for calculating domain and range.

For calculating the domain of piecewise function, together with the union of those three intervals from the three sub-functions conditions. So the domain=(-∞, 0)∪[0, 1]∪(1, ∞)=(-∞, ∞)

Calculating the range of this piecewise function:

For the First sub-function f(x)=x² where x<0 , we can get the range interval 0²+1<f(x)<(-∞)²+1 ⇒ 0<f(x)<∞

For the second sub-function f(x)=x where 0 ≤ x≤ 1 , we can get the range interval f(0) ≤ f(x) ≤ f(1) ⇒ 0 ≤ f(x) ≤ 1

For the Third sub-function f(x)=1/x where x>1 , we can get the range interval 1/f(∞) < f(x) < 1/f(1) ⇒ 1/∞ < f(x) < 1/1 ⇒ 0 < f(x) < 1

Now together with the union of this three range intervals, we get the range=(0, ∞)∪[0, 1]∪(0, 1)=[0, ∞)

Now again from the graph of this piecewise funtion, we see the graph is situated from left to right all over x-axis, so the domain=(-∞, ∞) and the graph is situated from origin to upper side all over the positive y-axis, so the range=[0,∞)

Domain and Range of a piecewise function can be guess from its graph.

Let us consider a piecewise function for calculating limit at a point is given belows.

The graph of this piecewise function for calculating limit at a point is given belows.

If we are calculating the limit of a piecewise defined function at the point where the function changes its sub-functions, then we will have to take one-sided limits separately named left hand limit (L.H.lim) and Right hand limit (R.H.lim) . If L.H.lim=R.H.lim, then the limit exist at that point , otherwise the limit does not exists at that point .

For calculating the lim_x->1 f(x), we will calculate left hand limit (L.H.lim) and Right hand limit (R.H.lim) at the point x=1. So at x=1, L.H.lim= lim_x->1^- f(x)=lim_x->1^- x²=1 and R.H.lim=lim_x->1⁺ f(x)=lim_x->1⁺ x=1. Since L.H.lim=R.H.lim at x=1, so the limit exist at x=1 and lim_x->1 f(x)=1

For calculating the lim_x->2 f(x), we will calculate left hand limit (L.H.lim) and Right hand limit (R.H.lim) at the point x=2. So at x=2, L.H.lim= lim_x->2^- f(x)=lim_x->2^- x=2 and R.H.lim=lim_x->2⁺ f(x)=lim_x->2⁺ (2x-1)=3. Since L.H.lim=R.H.lim at x=2, so the limit does not exist at x=2.

A piecewise Function that can be drawn without lifting up your pencil is called continuous piecewise functions. For calculating, If L.H.lim=R.H.lim=f(a) at x=a, then it is continuous at x=a otherwise it is discontinuous at x=a.

The graph of this piecewise function for calculating discontinuity at a point is given bellows-

For calculating the discontinuity of this piecewise function at x=1, we will calculate L.H.lim, R.H.lim at x=1 and the function value f(1). So at x=1, L.H.lim=lim_x->1^- f(x)=lim_x->1^- x²-4=1²-4=-3, R.H.lim=lim_x->1⁺ f(x)=lim_x->1⁺ -(1/2)x+1=-(1/2)(1)+1=1/2 and f(1)=-1. Since at x=1, L.H.lim≠R.H.lim≠f(1) , hence f(x) is discontinuous at x=1.

The graph of this piecewise function for calculating continuity at a point is given bellows-

For calculating the continuity of this piecewise function at x=4, we will calculate L.H.lim, R.H.lim at x=4 and the function value f(4). So at x=4, L.H.lim=lim_x->4^- f(x)=lim_x->4^- -x+5=-4+5=1, R.H.lim=lim_x->4⁺ f(x)=lim_x->4⁺ x-3=4-3=1 and f(4)=-4+5=1. Since at x=4, L.H.lim=R.H.lim=f(4)=1 , hence f(x) is continuous at x=4.

Let us consider two piecewise functions f(x) , g(x) and their graphs for create composite Piecewise functions or composition of piecewise functions are given belows.

we can divide the whole set of real numbers into three parts such as x<1, 1≤x<3 and x≥3.
Now for x<1, we get f(x)=x² and g(x)=2x. So the composite Piecewise functions or the composition of piecewise functions are (fog)(x)=f(g(x))=f(2x)=(2x)²=4x² and (gof)(x)=g(f(x))=g(x²)=2(x²)=2x²

Again for 1≤x<3, we get f(x)=2x+1 and g(x)=2x. So the composite Piecewise functions or the composition of piecewise functions are (fog)(x)=f(g(x))=f(2x)=2(2x)+1=4x+1 and (gof)(x)=g(f(x))=g(2x+1)=2(2x+1)=4x+2

Again for x≥3, we get f(x)=2x+1 and g(x)=2x²-1. So the composite functions or the composition of the functions are (fog)(x)=f(g(x))=f(2x²-1)=2(2x²-1)+1=4x²-1 and (gof)(x)=g(f(x))=g(2x+1)=2(2x+1)²-1=2(4x²+4x+1)-1=8x²+8x+1

Now combine for the three intervals, we get the composite Piecewise functions or composition of piecewise functions and their graphs are given belows.

Let us consider a absolute value function of multiple absolute value f(x)= |x-2| + |x-4|

we can divide the whole set of real numbers into three parts such as x<2, 2≤x<4 and x≥4.
By the definition of absolute value function, we get

Now for x<2, we get f(x)=|x-2| + |x-4|=-(x-2)+{-(x-4)}=-x+2-x+4=-2x+6.
Again for 2≤x<4, we get f(x)=|x-2| + |x-4|=(x-2)+ {-(x-4)} =x-2-x+4=2
Again for x≥4, we get f(x)= |x-2| + |x-4|=(x-2)+ (x-4) =2x-6
Now combine for the three intervals, we get the Piecewise functions and their graphs are given belows.

If f'(x)>0 on an interval, then function f(x) is increasing on that interval and if f'(x)<0 on an interval, then function f(x) is decreasing on that interval but if f'(x)=0 on an interval, then the function f(x) is neither increasing function nor decreasing function on that interval. As for example,

The first derivatives f'(x)=2x on an interval (1,∞). Now f'(x)>0 or 2x>0 or x>0, so f'(x)>0 on an interval (0,∞) that implies f'(x)>0 on an interval (1,∞).Hence the increasing interval (1,∞) of the function f(x). Again f'(x)<0 or 2x<0 or x<0, so f'(x)<0 on an interval (-∞, 0) that implies f'(x)<0 on an interval (-∞, -1). Hence the decreasing interval (-∞,-1) of the function f(x). But f'(x)=d(1)/dx=0 on the interval [-1,1], so f(x) is neither increasing nor decreasing on the interval [-1, 1]. The graph of the function f(x), increasing and decreasing interval is given belows.