This is an online educational tools (free online graphing calculator for math geogebra) to make graph of parametric functions of 2D. It can be used in science education. It is helpful of science students and teachers.Type any functions of x(t) and y(t) in the input boxes, then the graph will drawn automatically. It takes sometimes to draw graph of this function. If you need to write π, then you must write pi or PI or Pi
To get update website, you can clear your browser chache data (if you browse this website before many days) or browse this website with another website browser. Steps for clear chache: 1. on your computer, open browser. 2. At the top right, click More. 3. Click More tools. Clear browsing data. 4. choose a time range. 4. "Cached images and files," check the boxe. 5. Click Clear data. Different browser may have different ways.
parametric function represents with two functions x=f(t) and y=g(t) where t is a parameter. As for example, x=sin(t) and y=sin(2t) is a parametric functions. Free graphing calculator for math drawing website www.graph2d.com can draw any parametric functions. You can type sin(t)and sin(2t) in the input boxes and then the graph will drawn automatically of the graph. For learn about Mathematics functions and graphing, visit: Graphing Math functions.
Parametric equation is a set of equations, where the variables (usually x and y) are expressed in terms of a parameter, usually expressed as t. As for example, the equation of a circle x2+y2=32. This curve can be expressed as a Parametric equation: x(t)=3cos(t) and y(t)=3sin(t) where 0≤t<2π. Now drawing this parametric circle with parametric graphing calculator , type 3cos(t) in x(t) input box and 3cos(t) in y(t) input box, then the graph will drawn automatically and you can get a graph of circle. For learn about Piecewise functions of Mathematics and graphing, visit: Graphing Piecewise functions of Math.
Parametric equation of cardioid is x(t)= acost(1-cost) and y(t)= asint(1-cost) where a is constant. As for example,x(t)= 7cost(1-cost) and y(t)= 7sint(1-cost) is a equation of Parametric cardioid. Now drawing this parametric cardioid with parametric graphing calculator , type 7cos(t)(1-cos(t)) in x(t) input box and 7sin(t)(1-cos(t)) in y(t) input box, then the graph will drawn automatically and you can get a graph of cardioid. For learn about Complex Analysis of Mathematics and graphing, visit: Graphing Complex Analysis of Math.
Since x=at2, y=2at is satisfies the equation of parabola ( y2=4ax ), so the parametric equation of parabola is x(t)=at2, y(t)=2at.
Again consider an equation of ellipse x2/a2+y2/b2=1. Since x=acost and y=bsint is satisfy the equation of this ellepse, so the parametric equation of ellipse is x(t)=acost and y(t)=bsint.
Again consider an equation of Hyperbola x2/a2-y2/b2=1. Since x=asect and y=btant is satisfy the equation of this Hyperbola, so the parametric equation of Hyperbola is x(t)=acost and y(t)=bsint.
let us consider an equation of circle x2+y2=r2. Since x=rcost and y=rsint is satisfy the equation of this circle, so the parametric equation of circle is x(t)=rcost and y(t)=rsint.
The parametric equation of a cycloid is x=t−sint , y=1−cost. We want to compute the area under one arch of the cycloid. So Area under one arch of the cycloid is A=∫02π ydx but we do not know y in terms of x. We can substitute y=1−cost and compute dx=(1−cost)dt. So the area A=∫02π (1−cost)(1−cost)dt==3π square units.
Let us consider the parametric function x=f(t), y=g(t) for finding the asymptote of parallel to the co-ordinate axes. If t→t1, y=g(t)→∞ such that x→a then x=a is an asymptote. Again If t→t1, x=f(t)→∞ such that y→b then y=b is an asymptote.
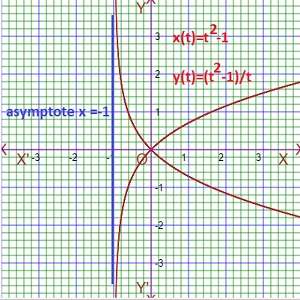
As for example, x(t)=t2-1 and y(t)=(t2-1)/t. When t→0 then y(t)→∞ or y(t)→-∞ such that x→-1, hence x=-1 is an asymptote of parametric function. The graph of this parametric function and its asymptote is given belows.
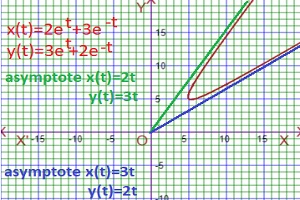
Again consider the parametric function x(t)=2et+3e-t and y(t)=3et+2e-t for finding oblique asymptote.If t→∞,then the slope=(dy/dt)/(dx/dt)=(3et-2e-t)/(2et-3e-t)=(3-2e-2t)/(2-3e-2t)→3/2, hence the asymptote will be y=(3/2)x ⇒2y=3x so the parametric equation of this asymptote is x(t)=2t and y(t)=3t. If t→-∞,then the slope=(dy/dt)/(dx/dt)=(3et-2e-t)/(2et-3e-t)=(3e2t-2)/(2e2t-3)→2/3, hence the asymptote will be y=(2/3)x ⇒3y=2x so the parametric equation of this asymptote is x(t)=3t and y(t)=2t. The graph of parametric function and its asymptotes are given belows.
